第三章 ArrayList
译者:飞龙
自豪地采用谷歌翻译
本章一举两得:我展示了上一个练习的解法,并展示了一种使用摊销分析来划分算法的方法。
3.1 划分MyArrayList的方法
对于许多方法,我们不能通过测试代码来确定增长级别。例如,这里是MyArrayList的get的实现:
public E get(int index) {
if (index < 0 || index >= size) {
throw new IndexOutOfBoundsException();
}
return array[index];
}
get中的每个东西都是常数时间的。所以get是常数时间,没问题。
现在我们已经划分了get,我们可以使用它来划分set。这是我们以前的练习中的set:
public E set(int index, E element) {
E old = get(index);
array[index] = element;
return old;
}
该解决方案的一个有些机智的部分是,它不会显式检查数组的边界;它利用get,如果索引无效则引发异常。
set中的一切,包括get的调用都是常数时间,所以set也是常数时间。
接下来我们来看一些线性的方法。例如,以下是我的实现indexOf:
public int indexOf(Object target) {
for (int i = 0; i<size; i++) {
if (equals(target, array[i])) {
return i;
}
}
return -1;
}
每次在循环中,indexOf调用equals,所以我们首先要划分equals。这里就是:
private boolean equals(Object target, Object element) {
if (target == null) {
return element == null;
} else {
return target.equals(element);
}
}
此方法调用target.equals;这个方法的运行时间可能取决于target或element的大小,但它不依赖于该数组的大小,所以出于分析indexOf的目的,我们认为这是常数时间。
回到之前的indexOf,循环中的一切都是常数时间,所以我们必须考虑的下一个问题是:循环执行多少次?
如果我们幸运,我们可能会立即找到目标对象,并在测试一个元素后返回。如果我们不幸,我们可能需要测试所有的元素。平均来说,我们预计测试一半的元素,所以这种方法被认为是线性的(除了在不太可能的情况下,我们知道目标元素在数组的开头)。
remove的分析也类似。这里是我的时间。
public E remove(int index) {
E element = get(index);
for (int i=index; i<size-1; i++) {
array[i] = array[i+1];
}
size--;
return element;
}
它使用get,这是常数时间,然后从index开始遍历数组。如果我们删除列表末尾的元素,循环永远不会运行,这个方法是常数时间。如果我们删除第一个元素,我们遍历所有剩下的元素,它们是线性的。因此,这种方法同样被认为是线性的(除了在特殊情况下,我们知道元素在末尾,或到末尾距离恒定)。
3.2 add的划分
这里是add的一个版本,接受下标和元素作为参数:
public void add(int index, E element) {
if (index < 0 || index > size) {
throw new IndexOutOfBoundsException();
}
// add the element to get the resizing
add(element);
// shift the other elements
for (int i=size-1; i>index; i--) {
array[i] = array[i-1];
}
// put the new one in the right place
array[index] = element;
}
这个双参数的版本,叫做add(int, E),它使用了单参数的版本,称为add(E),它将新的元素放在最后。然后它将其他元素向右移动,并将新元素放在正确的位置。
在我们可以划分双参数add之前,我们必须划分单参数add:
public boolean add(E element) {
if (size >= array.length) {
// make a bigger array and copy over the elements
E[] bigger = (E[]) new Object[array.length * 2];
System.arraycopy(array, 0, bigger, 0, array.length);
array = bigger;
}
array[size] = element;
size++;
return true;
}
单参数版本很难分析。如果数组中存在未使用的空间,那么它是常数时间,但如果我们必须调整数组的大小,它是线性的,因为System.arraycopy所需的时间与数组的大小成正比。
那么add是常数还是线性时间的?我们可以通过考虑一系列n个添加中,每次添加的平均操作次数,来分类此方法。为了简单起见,假设我们以一个有2个元素的空间的数组开始。
- 我们第一次调用
add时,它会在数组中找到未使用的空间,所以它存储1个元素。 - 第二次,它在数组中找到未使用的空间,所以它存储
1个元素。 - 第三次,我们必须调整数组的大小,复制
2个元素,并存储1个元素。现在数组的大小是4。 - 第四次存储
1个元素。 - 第五次调整数组的大小,复制
4个元素,并存储1个元素。现在数组的大小是8。 - 接下来的
3个添加储存3个元素。 - 下一个添加复制
8个并存储1个。现在的大小是16。 - 接下来的
7个添加复制了7个元素。
以此类推,总结一下:
4次添加之后,我们储存了4个元素,并复制了两个。8次添加之后,我们储存了8个元素,并复制了6个。16次添加之后,我们储存了16个元素,并复制了14个。
现在你应该看到了规律:要执行n次添加,我们必须存储n个元素并复制n-2个。所以操作总数为n + n - 2,为2 * n - 2。
为了得到每个添加的平均操作次数,我们将总和除以n;结果是2 - 2 / n。随着n变大,第二项2 / n变小。参考我们只关心n的最大指数的原则,我们可以认为add是常数时间的。
有时线性的算法平均可能是常数时间,这似乎是奇怪的。关键是我们每次调整大小时都加倍了数组的长度。这限制了每个元素被复制的次数。否则 - 如果我们向数组的长度添加一个固定的数量,而不是乘以一个固定的数量 - 分析就不起作用。
这种划分算法的方式,通过计算一系列调用中的平均时间,称为摊销分析。你可以在 http://thinkdast.com/amort 上阅读更多信息。重要的想法是,复制数组的额外成本是通过一系列调用展开或“摊销”的。
现在,如果add(E)是常数时间,那么add(int, E)呢?调用add(E)后,它遍历数组的一部分并移动元素。这个循环是线性的,除了在列表末尾添加的特殊情况中。因此, add(int, E)是线性的。
3.3 问题规模
最后一个例子中,我们将考虑removeAll,这里是MyArrayList中的实现:
public boolean removeAll(Collection<?> collection) {
boolean flag = true;
for (Object obj: collection) {
flag &= remove(obj);
}
return flag;
}
每次循环中,removeAll都调用remove,这是线性的。所以认为removeAll是二次的很诱人。但事实并非如此。
在这种方法中,循环对于每个collection中的元素运行一次。如果collection包含m个元素,并且我们从包含n个元素的列表中删除,则此方法是O(nm)的。如果collection的大小可以认为是常数,removeAll相对于n是线性的。但是,如果集合的大小与n成正比,removeAll则是平方的。例如,如果collection总是包含100个或更少的元素, removeAll则是线性的。但是,如果collection通常包含的列表中的 1% 元素,removeAll则是平方的。
当我们谈论问题规模时,我们必须小心我们正在讨论哪个大小。这个例子演示了算法分析的陷阱:对循环计数的诱人捷径。如果有一个循环,算法往往是 线性的。如果有两个循环(一个嵌套在另一个内),则该算法通常是平方的。不过要小心!你必须考虑每个循环运行多少次。如果所有循环的迭代次数与n成正比,你可以仅仅对循环进行计数之后离开。但是,如在这个例子中,迭代次数并不总是与n成正比,所以你必须考虑更多。
3.4 链接数据结构
对于下一个练习,我提供了List接口的部分实现,使用链表来存储元素。如果你不熟悉链表,你可以阅读 http://thinkdast.com/linkedlist ,但本部分会提供简要介绍。
如果数据结构由对象(通常称为“节点”)组成,其中包含其他节点的引用,则它是“链接”的。在链表 中,每个节点包含列表中下一个节点的引用。其他链接结构包括树和图,其中节点可以包含多个其他节点的引用。
这是一个简单节点的类定义:
public class ListNode {
public Object data;
public ListNode next;
public ListNode() {
this.data = null;
this.next = null;
}
public ListNode(Object data) {
this.data = data;
this.next = null;
}
public ListNode(Object data, ListNode next) {
this.data = data;
this.next = next;
}
public String toString() {
return "ListNode(" + data.toString() + ")";
}
}
该ListNode对象具有两个实例变量:data是某种类型的Object的引用,并且next是列表中下一个节点的引用。在列表中的最后一个节点中,按照惯例,next是null。
ListNode提供了几个构造函数,可以让你为data和next提供值,或将它们初始化为默认值,null。
你可以将每个ListNode看作具有单个元素的列表,但更通常,列表可以包含任意数量的节点。有几种方法可以制作新的列表。一个简单的选项是,创建一组ListNode对象,如下所示:
ListNode node1 = new ListNode(1);
ListNode node2 = new ListNode(2);
ListNode node3 = new ListNode(3);
之后将其链接到一起,像这样:
node1.next = node2;
node2.next = node3;
node3.next = null;
或者,你可以创建一个节点并将其链接在一起。例如,如果要在列表开头添加一个新节点,可以这样做:
ListNode node0 = new ListNode(0, node1);
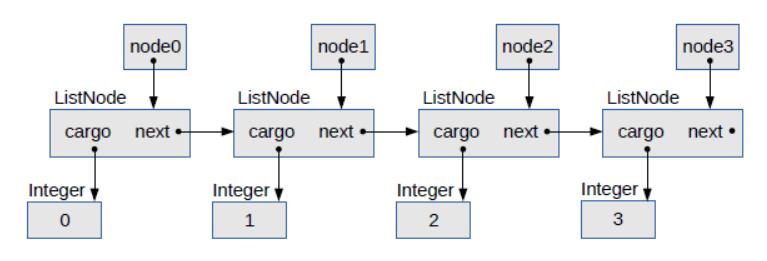
图 3.1 链表的对象图
图 3.1 是一个对象图,展示了这些变量及其引用的对象。在对象图中,变量的名称出现在框内,箭头显示它们所引用的内容。对象及其类型(如ListNode和Integer)出现在框外面。
3.5 练习 3
这本书的仓库中,你会找到你需要用于这个练习的源代码:
MyLinkedList.java包含List接口的部分实现,使用链表存储元素。MyLinkedListTest.java包含用于MyLinkedList的 JUnit 测试。
运行ant MyArrayList来运行MyArrayList.java,其中包含几个简单的测试。
然后可以运行ant MyArrayListTest来运行 JUnit 测试。其中几个应该失败。如果你检查源代码,你会发现三条 TODO 注释,表示你应该填充的方法。
在开始之前,让我们来看看一些代码。以下是MyLinkedList的实例变量和构造函数:
public class MyLinkedList<E> implements List<E> {
private int size; // keeps track of the number of elements
private Node head; // reference to the first node
public MyLinkedList() {
head = null;
size = 0;
}
}
如注释所示,size跟踪MyLinkedList有多少元素;head是列表中第一个Node的引用,或者如果列表为空则为null。
存储元素数量不是必需的,并且一般来说,保留冗余信息是有风险的,因为如果没有正确更新,就有机会产生错误。它还需要一点点额外的空间。
但是如果我们显式存储size,我们可以实现常数时间的size方法;否则,我们必须遍历列表并对元素进行计数,这需要线性时间。
因为我们显式存储size明确地存储,每次添加或删除一个元素时,我们都要更新它,这样一来,这些方法就会减慢,但是它不会改变它们的增长级别,所以很值得。
构造函数将head设为null,表示空列表,并将size设为0。
这个类使用类型参数E作为元素的类型。如果你不熟悉类型参数,可能需要阅读本教程:http://thinkdast.com/types。
类型参数也出现在Node的定义中,嵌套在MyLinkedList里面:
private class Node {
public E data;
public Node next;
public Node(E data, Node next) {
this.data = data;
this.next = next;
}
}
除了这个,Node类似于上面的ListNode。
最后,这是我的add的实现:
public boolean add(E element) {
if (head == null) {
head = new Node(element);
} else {
Node node = head;
// loop until the last node
for ( ; node.next != null; node = node.next) {}
node.next = new Node(element);
}
size++;
return true;
}
此示例演示了你需要的两种解决方案:
对于许多方法,作为特殊情况,我们必须处理列表的第一个元素。在这个例子中,如果我们向列表添加列表第一个元素,我们必须修改head。否则,我们遍历列表,找到末尾,并添加新节点。
此方法展示了,如何使用for循环遍历列表中的节点。在你的解决方案中,你可能会在此循环中写出几个变体。注意,我们必须在循环之前声明node,以便我们可以在循环之后访问它。
现在轮到你了。填充indexOf的主体。像往常一样,你应该阅读文档,位于 http://thinkdast.com/listindof,所以你知道应该做什么。特别要注意它应该如何处理null。
与上一个练习一样,我提供了一个辅助方法equals,它将数组中的一个元素与目标值进行比较,并检查它们是否相等,并正确处理null。这个方法是私有的,因为它在这个类中使用,但它不是List接口的一部分。
完成后,再次运行测试;testIndexOf,以及依赖于它的其他测试现在应该通过。
接下来,你应该填充双参数版本的add,它使用索引并将新值存储在给定索引处。再次阅读 http://thinkdast.com/listadd 上的文档,编写一个实现,并运行测试进行确认。
最后一个:填写remove的主体。文档在这里:http://thinkdast.com/listrem。当你完成它时,所有的测试都应该通过。
一旦你的实现能够工作,将它与仓库solution目录中的版本比较。
3.6 垃圾回收的注解
在MyArrayList以前的练习中,如果需要,数字会增长,但它不会缩小。该数组从不收集垃圾,并且在列表本身被销毁之前,元素不会收集垃圾。
链表实现的一个优点是,当元素被删除时它会缩小,并且未使用的节点可以立即被垃圾回收。
这是我的实现的clear方法:
public void clear() {
head = null;
size = 0;
}
当我们将head设为null时,我们删除第一个Node的引用。如果没有其他Node的引用(不应该有),它将被垃圾收集。这个时候,第二个Node引用被删除,所以它也被垃圾收集。此过程一直持续到所有节点都被收集。
那么我们应该如何划分clear?该方法本身包含两个常数时间的操作,所以它看起来像是常数时间。但是当你调用它时,你将使垃圾收集器做一些工作,它与元素数成正比。所以也许我们应该将其认为是线性的!
这是一个有时被称为性能 bug 的例子:一个程序做了正确的事情,在这种意义上它是正确的,但它不属于我们预期的增长级别。在像 Java 这样的语言中,它在背后做了大量工作的,例如垃圾收集,这种 bug 可能很难找到。

